MNIST 간단 예제
from sklearn.datasets import fetch_mldata
mnist = fetch_openml('mnist_784')
mnist기존 책에 있는 소스코드에서는 fetch_openml이 정의되어 있지 않다는 error가 발생
아래의 아주 조금 수정된 코드를 첨부한다.
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784')
mnist.data.shape, mnist.target.shape
from sklearn.datasets import fetch_openml
mnist = fetch_openml('mnist_784')
mnist.data.shape, mnist.target.shape
X,y = mnist["data"],mnist["target"]
X.shape
y.shape
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
some_digit = X[36000] #36000index에 해당하는 수는 9이며 아래 5-분류기에서 쓰일 5는 35 등이 있다.
some_digit_image = some_digit.reshape(28,28)
plt.imshow(some_digit_image, cmap = matplotlib.cm.binary,interpolation="nearest")
plt.axis("off")
plt.show()
y[36000]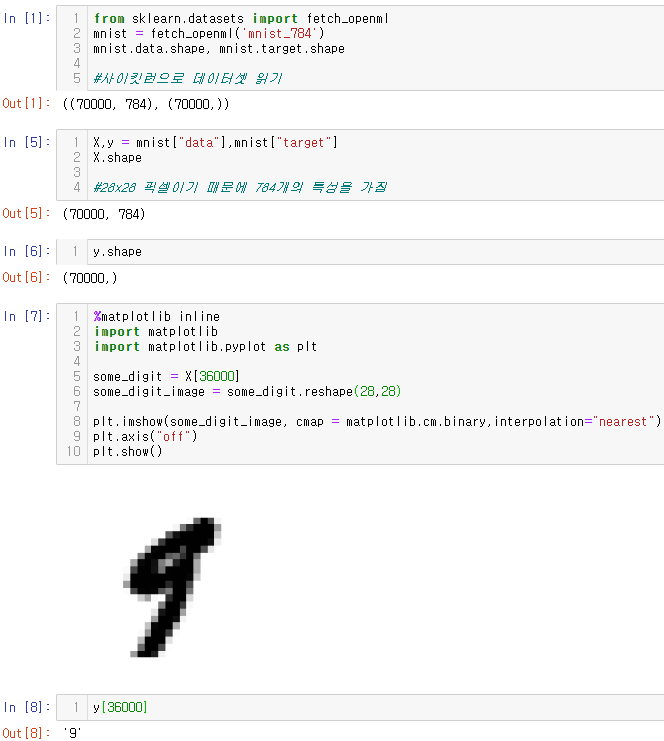
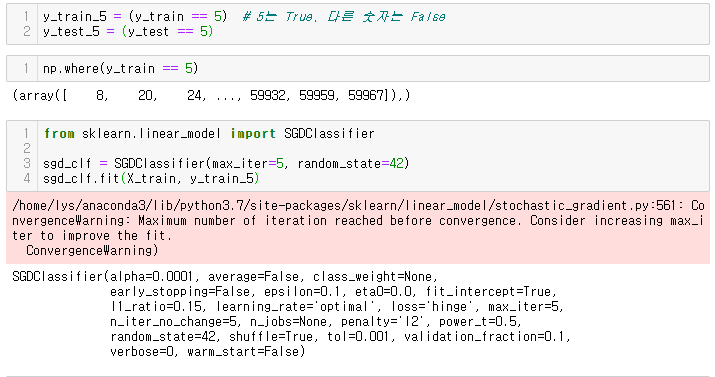
X_train, X_test, y_train, y_test = X[:60000], X[60000:], y[:60000], y[60000:]
import numpy as np
shuffle_index = np.random.permutation(60000)
X_train, y_train = X_train[shuffle_index], y_train[shuffle_index]
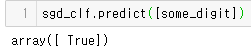
y_train_5 = (y_train == 5) # 5는 True, 다른 숫자는 False
y_test_5 = (y_test == 5)
from sklearn.linear_model import SGDClassifier
sgd_clf = SGDClassifier(max_iter=5, random_state=42)
sgd_clf.fit(X_train, y_train_5)
sgd_clf.predict([some_digit])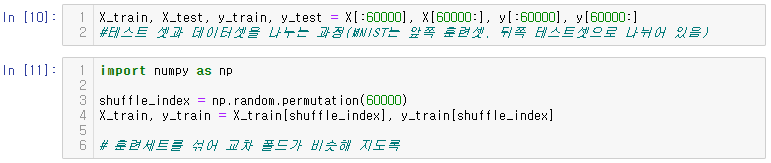
이진 분류기 훈련
이진 분류기 - 두 개의 클래스를 구분하는 분류기
예제) 5-감지기 - 숫자 5만 식별
- 5, 5 아님 두 개의 클래스를 구분하는 이진분류기
성능측정
교차 검증을 사용한 정확도 측정
from sklearn.model_selection import cross_val_score
cross_val_score(sgd_clf, X_train, y_train_5, cv=3, scoring='accuracy')
# 폴드가 3개인 k-겹 교차 검증 사용
# cross_val_score()함수와 거의 같은 작업을 수행하는 코드
# 사이킷런에서 제공하는 기능보다 교차 검증 과정을 더 많에 제어해야 할 경우
# 아래처럼 교차 검증 기능을 직접 구현
#-----------------------------------#
from sklearn.model_selection import StratifiedKFold
from sklearn.base import clone
skfolds = StratifiedKFold(n_splits=3, random_state=42)
for train_index, test_index in skfolds.split(X_train, y_train_5):
clone_clf = clone(sgd_clf) # sgd_clf 복제
X_train_folds = X_train[train_index]
y_train_folds = (y_train_5[train_index])
X_test_fold = X_train[test_index]
y_test_fold = (y_train_5[test_index])
clone_clf.fit(X_train_folds, y_train_folds)
y_pred = clone_clf.predict(X_test_fold)
n_correct = sum(y_pred == y_test_fold)
print(n_correct / len(y_pred))

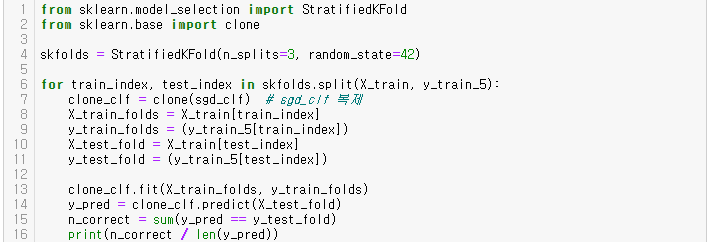


위 교차검증 폴드에 대한 정확도는 95% 이상이다.
5-감지기를 통해 5/5 아닌 클래스를 분류하는 더미 분류기 코드, 모델의 정확도 추측
from sklearn.base import BaseEstimator
class Never5Classifier(BaseEstimator):
def fit(self, X, y=None):
pass
def predict(self, X):
return np.zeros((len(X), 1), dtype=bool)
never_5_clf = Never5Classifier()
cross_val_score(never_5_clf, X_train, y_train_5, cv=3, scoring="accuracy")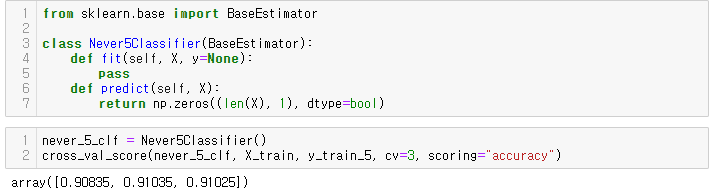
위 예제는 정확도가 90% 이상이다( ** 이미지의 10%만이 5이기 때문에 5아님으로 예측시 맞출확률이 90% 이상이다 )
위 예제는 정확도를 분류기의 성능 측정 지표로 선호하지 않는 이유를 보여준다.(특히 불균형한 데이터셋)
오차행렬
클래스 A의 샘플이 클래스 B로 분류된 횟수를 세는 것
ex) 분류기가 숫자5의 이미지를 3으로 잘못 분류한 횟수를 알고 싶을 때 오차 행렬의 5행 3열을 본다
오차행렬 생성 전 실제 target과 비교를 위한 예측값 생성
from sklearn.model_selection import cross_val_predict
y_train_pred = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3)
# cross_val_predict() 를 활용하여
# K-겹 교차 검증 수행, 각 테스 폴드에서 얻은 예측 반환
from sklearn.metrics import confusion_matrix
confusion_matrix(y_train_5, y_train_pred)
# 타깃 클래스 - y_train_5 / 예측클래스 - y_train_pred
confusion_matrix(y_train_5, y_train_5)
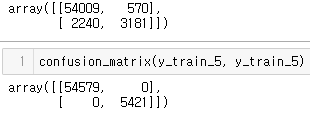
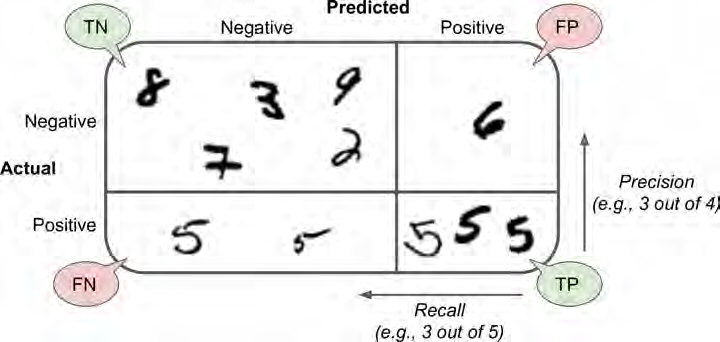
- TP: True-Positive, 1이라고 예측했는데, 실제로도 1인 경우 →정답
- TN: True-Negative, 0이라고 예측했는데, 실제로도 0일 경우 →정답
- FP: False-Positive, 1이라고 예측했는데, 실제로는 0인 경우
- FN: False-Negative, 0이라고 예측했는데, 실제로는 1인 경우
정밀도(precision) = 오차 행렬보다 더 요약된 지표, 양성 예측의 정확도 $ { TP \over TP+FP} $
재현률(recall) = 분류기가 정확하게 감지한 양성 샘플의 비율 ${ TP \over TP+FN}$
정밀도와 재현율
정밀도
precision = 4432 / (4432 + 1607)
precision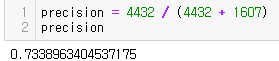
재현율
from sklearn.metrics import precision_score, recall_score
precision_score(y_train_5, y_train_pred)
$F_1$점수($F_1$score) - 정밀도와 재현율의 조화 평균(harmonic mean)
$F_1 = {2 \over {1 \over 정밀도} + {1 \over 재현율}} = 2x {정밀도x재현율 \over 정밀도+재현율} = {TP \over {tp + {FN+FP} \over 2}}$
f1_score_ = 4432 / (4432 + (989 + 1607)/2)
f1_score_
from sklearn.metrics import f1_score
f1_score(y_train_5, y_train_pred)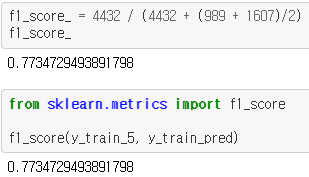
정밀도/재현율 트레이드오프
정밀도와 재현율은 서로 반비례한다.
정밀도와 재현율은 상황에 따라 중요도가 다르다.
- i.e. 어린이 안전유해 영상 분류기( 낮은 재현율/높은 정밀도가 중요 - 좋은 동영상이 많이 제외되더라도 안전한 영상만 노출)
- i.e. 도둑잡는 감시카메라 분류기( 높은 재현율/낮은 정밀도(상대적) ) - 호출이 자주 되겠지만 도둑을 잡는 분류
SGDClassifier와 정밀도/재현율 트레이드오프
SGDClassifier는 결정 함수(decision function)를 사용하여 각 샘플의 점수 계산
계산한 점수가 임계값보다 크면 샘플을 양성 클래스에 할당/ 아닐경우 음성 클래스에 할당

- (5|5) 가운데 화살표를 임계값이라 가정
- 화살표 기준 오른쪽 5(정답)4개, 6(오답) 1개 : 4/5 = 80%정밀도
- 실제 5(정답)의 갯수 6개, 분류기가 감지한 5(정답)의 갯수 4개 : 4/6 = 67%재현율
- (6|5) 가운데 화살표를 임계값이라 가정
- 화살표 기준 오른쪽 5(정답)3개, 오답 없음 : 3/3 = 100%정밀도
- 위에서 FP로 분류한 6이 TN이 되어 정밀도 상승 = 3/6 = 50%재현율
- (9|5) 가운데 화살표를 임계값이라 가정
- 화살표 기준 오른쪽 5(정답)6개, 2,6(오답)2개 : 6/8 = 75%정밀도
- 실제 정답(5)의 갯수 : 6, 분류기가 탐지한 정답(5)의 갯수 : 6 = 6/6 = 100%재현율
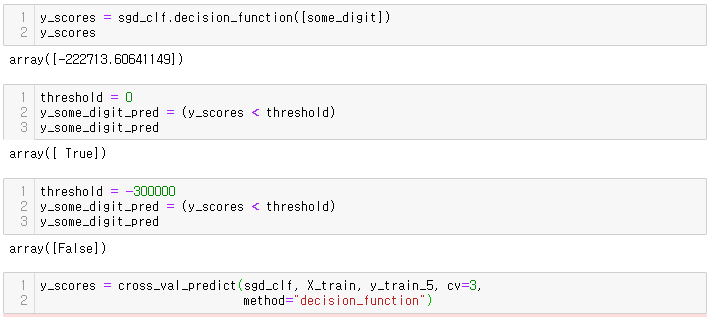
y_scores = sgd_clf.decision_function([some_digit])
y_scores
threshold = 0
y_some_digit_pred = (y_scores < threshold)
y_some_digit_pred
threshold = -300000 # 임계값 조정
y_some_digit_pred = (y_scores < threshold)
y_some_digit_pred
y_scores = cross_val_predict(sgd_clf, X_train, y_train_5, cv=3,
method="decision_function")
#적절한 임계값을 얻기 위해 모든 결졍 점수를 반환
from sklearn.metrics import precision_recall_curve
precisions, recalls, thresholds = precision_recall_curve(y_train_5, y_scores)
#precision_recall_curve()를 사용하여 정밀도, 재현율 계산
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
# b-- 정밀도/g- 재현율 그래프로 표현
plt.plot(thresholds, precisions[:-1], "b--", label="정밀도", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="재현율", linewidth=2)
plt.xlabel("임계값", fontsize=16)
plt.legend(loc="upper left", fontsize=16)
plt.ylim([0, 1])
plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
plt.show()
def plot_precision_recall_vs_threshold(precisions, recalls, thresholds):
# 정밀도(y), 재현율(x) 그래프
plt.plot(thresholds, precisions[:-1], "b--", label="정밀도", linewidth=2)
plt.plot(thresholds, recalls[:-1], "g-", label="재현율", linewidth=2)
plt.xlabel("임계값", fontsize=16)
plt.legend(loc="upper left", fontsize=16)
plt.ylim([0, 1])
plt.figure(figsize=(8, 4))
plot_precision_recall_vs_threshold(precisions, recalls, thresholds)
plt.xlim([-700000, 700000])
plt.show()
적절한 임계값 찾기위한 과정
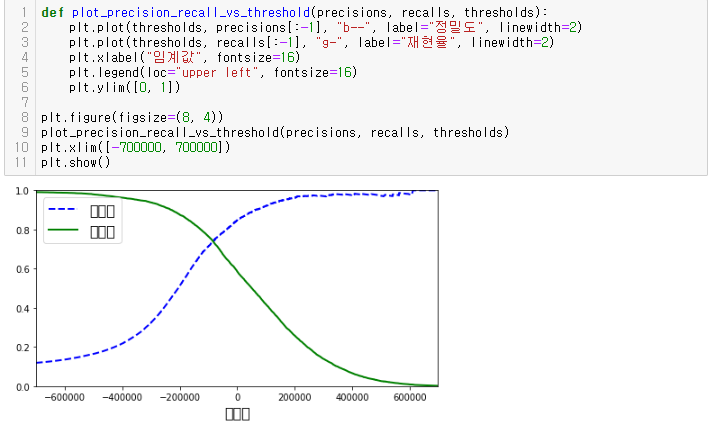
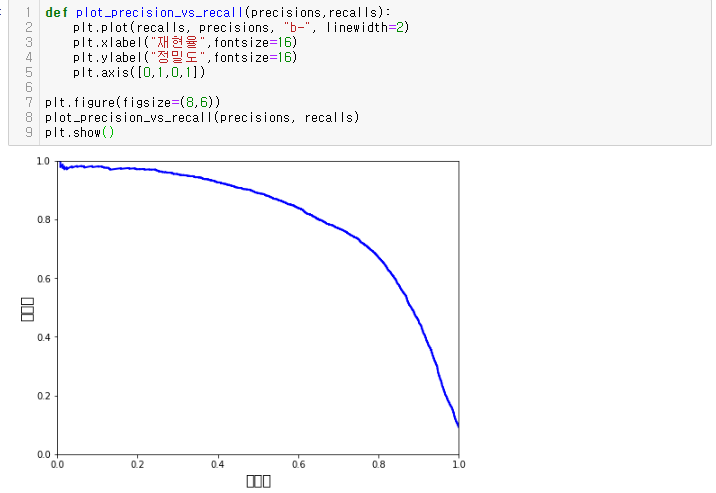
프로젝트에 따라 다르겠지만 일반적으로 Precision/Recall Trade-off는 위의 그래프에서 하강점 직전, 즉 0.6(60%) 지점을 선택하는 것이 좋다.
ROC(receiver operating characteristic) 곡선
- 수신기 조작 특성 곡선 - 거짓 양성비율(False Positive Rate)에 대한 진짜 양성 비율(True Positive Rate)의 곡선
- 민감도(재현율)에 대한 1-특이도 그래프
- FPR : 양성으로 잘못 분류된 음성 샘플의 비율
- TPR : 1 - 정확하게 분류한 음성 샘플의 비율(True Negative Rate)
- TNR : 특이도(specificity)
from sklearn.metrics import roc_curve
fpr, tpr, thresholds = roc_curve(y_train_5, y_scores)
def plot_roc_curve(fpr, tpr, label=None):
plt.plot(fpr, tpr, linewidth=2, label=label)
plt.plot([0, 1], [0, 1], 'k--')
plt.axis([0, 1, 0, 1])
plt.xlabel('FPR', fontsize=16)
plt.ylabel('TPR', fontsize=16)
plt.figure(figsize=(8, 6))
plot_roc_curve(fpr, tpr)
plt.show()
from sklearn.metrics import roc_auc_score
roc_auc_score(y_train_5, y_scores)
from sklearn.ensemble import RandomForestClassifier
forest_clf = RandomForestClassifier(random_state=42)
y_probas_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3,
method="predict_proba")
y_scores_forest = y_probas_forest[:, 1] # 점수는 양성 클래스의 확률
fpr_forest, tpr_forest, thresholds_forest = roc_curve(y_train_5,y_scores_forest)
plt.figure(figsize=(8, 6))
plt.plot(fpr, tpr, "b:", linewidth=2, label="SGD")
plot_roc_curve(fpr_forest, tpr_forest, "랜덤 포레스트")
plt.legend(loc="lower right", fontsize=16)
plt.show()
roc_auc_score(y_train_5, y_scores_forest)
y_train_pred_forest = cross_val_predict(forest_clf, X_train, y_train_5, cv=3)
precision_score(y_train_5, y_train_pred_forest)
recall_score(y_train_5, y_train_pred_forest)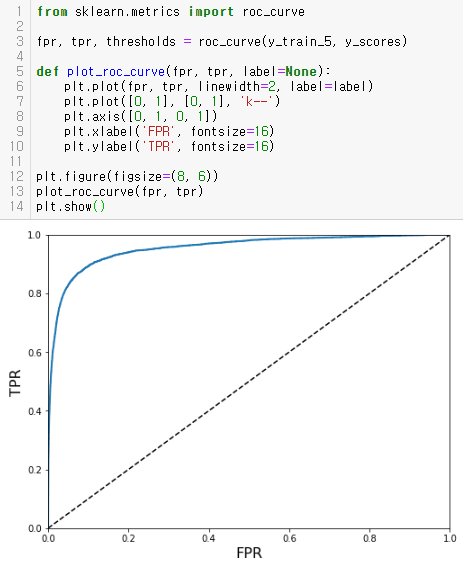
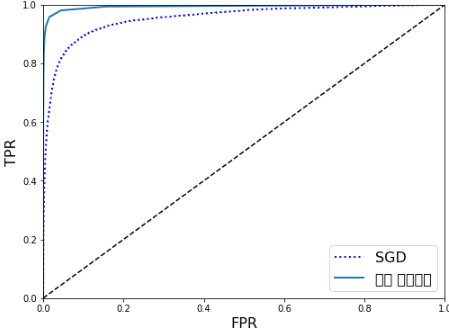
TPR(재현율)이 높을수록 FPR이 증가/성능이 좋은 분류기는 점선에서 부터 최대한 멀리 떨어져야한다(왼쪽 위 모서리)
AUC
- 분류기 성능비교 지표
- 1에 가까울수록 좋은 분류기
다중분류(multiclass/multinomial classification) - 둘 이상의 클래스 분류
OvA(One versus All, One versus the rest, OVR) - 일대다 방법
- 특정 클래스 하나만 분류하는 방법
- 이진 분류기 10개를 만들어 그 중 가장 높은 확률값을 가지는 클래스로 분류하는 방법
OvO(One versus One) - 일대일 방법
- 각 클래스의 조합마다 이진 분류기를 만들어 학습시키는 방법
- 클래스가 N개일 경우 $ {N * (N-1) \over 2} $개 필요
에러 분석
- cross_val_predict()함수를 사용해 예측 생성 - confusion_matrix()함수 호출하여 오차 행렬 확인
- 오차 행렬의 각 값이 대응되는 클래스의 이미지 개수로 나누어 에러 비율 비교
다중 레이블 분류 - 여러개의 이진 레이블을 출력하는 분류 시스템
다중 출력 분류 - 다중 레이블 분류에서 한 레이블이 다중 클래스가 될 수 있도록 일반화
#본 게시물은 hands on machine learning with Scikit-Learn & TensorFlow 를 읽고 게시하였습니다. #
'핸즈온 머신러닝' 카테고리의 다른 글
| Chapter 5 서포트 벡터 머신(svm) (0) | 2020.09.18 |
|---|---|
| Chapter4 모델 훈련 (0) | 2020.09.17 |
| CHAPTER 2 머신러닝 프로젝트 처음부터 끝까지 (0) | 2020.03.26 |
| CHAPTER 1 한눈에 보는 머신러닝 (0) | 2020.03.25 |



댓글