[논문 리뷰] Rapidly Generate and Visualize the Digest of Massive Time Series Data

오늘의 논문은 시계열 데이터의 시각화 방법을 찾아보던 중 읽게 된 논문이다.

오래전 읽고 이제야 포스팅을 하게 되었다... 만만하게 읽다 어려워 여러 번 다시 읽었고

포스팅을 하는 지금에서도 이해가 안가는 부분이 많아 참고 논문 등을 찾아 읽어 봐야 할 듯하다.

2017년 IEEE Third International Conference on Big Data Computing Service and Applications에 게재된 "Rapidly Generate and Visualize the Digest of Massive Time Series Data" 은 대량의 시계열 데이터를 요약하여 시각화하였다.

Abstract

시계열 데이터는 시간순으로 자주 수집되는 데이터 집합으로, 방대한 양이 관측과 활용에 어려움이 많다
본 논문에서는 방대한 시계열 데이터의 요약문을 신속하게 생성하여 시각화하는 방법을 제시한다.
- 방법
  1. 입력 시계열 데이터 선형 스캔
  2. 시계열 데이터를 데이터 간격의 복수도로 분할
  3. 통계 데이터 계산
  4. 각 간격의 데이터 특징 특성화
  5. 데이터 시리즈의 추세와 분포를 보여주기 위해 개선된 촛대 차트를 채택
이 방법은 적은 양의 데이터로 덜 복잡하며 관계형 데이터베이스에 데이터를 저장하고 조회 가능하며
촛대 차트의 개선된 시각화 방법은 촛대 차트에 나타난 색 변화를 통한 데이터 분포를 시각화 가능하여 실용적으로 확인이 가능하다.
또한 원본 데이터를 크게 압축하여 압축된 데이터를 바탕으로 비율에 따라 계층적으로 표시 가능하다.

1. Introduction

시계열 데이터는 시간순으로 수집된 데이터 집합으로 기상자료, 주식거래 정보 등 사회생활의 다양한 분야에 존재하며 처리와 분석이 점점 중요해지고 있다.
본 논문에서는 기존 데이터 애플리케이션 대부분이 관계형 데이터베이스를 기반으로 한다는 점을 감안하여 대용량 시계열 데이터 요약문을 신속하게 생성하고 시각화 방법을 제시한다.
이 방법은 입력된 시계열 데이터를 선형 스캔하고 시계열 데이터를 데이터 간격으로 분할하여 각 구간에서 데이터 특징을 나타내는 통계 데이터를 계산하고 시각적 시각화에 대한 데이터 시리즈의 경향과 분포를 보여주기 위해 개선된 촛대 차트를 채택하는 단계로 구성된다
이 방법은 원본 데이터를 크게 압축할 수 있으며, 압축된 데이터를 바탕으로 비율에 따라 이러한 데이터를 계층적으로 추가로 표시할 수 있다.
그런 다음 관계형 데이터베이스를 사용하여 데이터를 저장하고 조건부 검색을 지원하는데, 이는 서로 다른 장면과 요건에 적합한 시각화 방법을 제공한다.
또한 변동 및 분포에 대한 데이터 특성을 고려하여 대규모 시계열 데이터의 시각화 효과를 개선하는 촛대 차트의 개선된 시각화 방법을 제안한다.

2. The preprocessing of time series data

전처리 : 시계열 데이터를 간격 목록으로 변환 ( 본 논문에선 데이터 간격 특성(PLR DIF)에 기반한 PLR 제안 )
PLR DIF에서의 데이터 간격은 $ I = < t_s , t_e , v_s , v_e , v_{max} , v_{min} , v_{arg} , E >$ 로 정의된다.
- $t_s , t_e $ : 데이터 간격 구간의 시작, 종료 시간
- $v_s, v_e $ : 첫 번째 데이터 값과 마지막 데이터 값
- $v_max , v_min, v_avg, v_avr $ : 최댓값, 최솟값, 평균, 표준편차
- $ E : $ 구간 내 데이터 분포를 유지하는 벡터
각 데이터의 간격 : 평균적으로 $v_{min} ~ v_{max}$까지 P간격으로 구분
각 값 간격의 데이터 수는 크기별 벡터 E에 카운트되어 저장된다.

2-A. The processing of one-dimensional time series data

M의 간격을 가진 시계열 데이터의 전처리 목적 : N개의 연속적인 데이터 포인트를 선형 스캔 수행하는 것이다.
이 과정에서 데이터 포인트의 통계적 특성이 계산된 후 데이터 간격을 압축된다.
첫 번째 데이터, 마지막 데이터, 최대, 최소, 평균 및 표준 편차는 데이터의 기본 특성을 구간별로 반영하기 때문에 선택되며, 이러한 통계 데이터는 구간 병합되는 동안 좋은 성능을 보인다.
즉, 병합된 데이터 구간의 통계 특성 값은 인접한 두 구간의 통계 특성 값에 따라 계산할 수 있다.

$D_1, D_2, D_3$ 및 $D_4$ : 동일한 시스템에서 수집한 4차원 시계열 데이터
ex) $D_4$
- 간격(M)을 800으로 설정
- 시계열 데이터를 순차적으로 스캔
- 시작 데이터 포인트, 끝 데이터 포인트를 저장
- $D_4$ 열 데이터에서 각 구간 $M_i$ (i = 1,2, ..., k)에 대한 최대, 최소, 평균, 표준 편차 및 데이터 분포 계산

표 2는 $D_4$의 출력 결과이다.
간격(M)이 800으로 되어있다.
이에 따라 시작, 종료, 평균... 의 값들이 각각 저장되고 계산된다.

2-B. The processing of high-dimensional time series data

실용적인 애플리케이션에는 항상 고차원 시계열 데이터의 주소 지정이 포함되기 때문에 동시에 여러 센서에서 수집된 데이터를 저장, 추가로 분석해야 한다.
본 논문에서는 처리를 위해 고차원 시계열 데이터를 여러 개의 1차원 데이터로 나누고 총 데이터 차원 수를 d라고 가정합니다.
- 원래 데이터 레코드의 총 수 : N
- 시간 t에서 i 차원의 데이터 : $d_{ti}$
- 총 데이터 저장 용량 : $S = N \times d \times B $ (식 1)
  - B : 각 데이터 $d_{ti}$가 차지하는 공간의 크기(바이트)
제안된 방법을 사용하여 시계열 데이터를 저장하는 경우
- 각 구간에서 원본 데이터 설명 위한 11개의 속성 필요
  - 열 번호
  - 간격 번호
  - 간격 시작, 종료 시간
  - 첫 번째 데이터 값, 마지막 데이터 값
  - 최댓값, 최솟값, 평균, 표준편차
전처리 후 데이터의 크기 : $S = N \times(9+P)/M \times d \times B $ (식 2)
- M : 간격
- P : 각 간격에서 데이터 분포를 유지하는데 필요한 데이터 수
식 1,2 : 압축 비율이 M의 크기에 의존
- M을 조정하여 여러 압축 비율을 얻을 수 있음

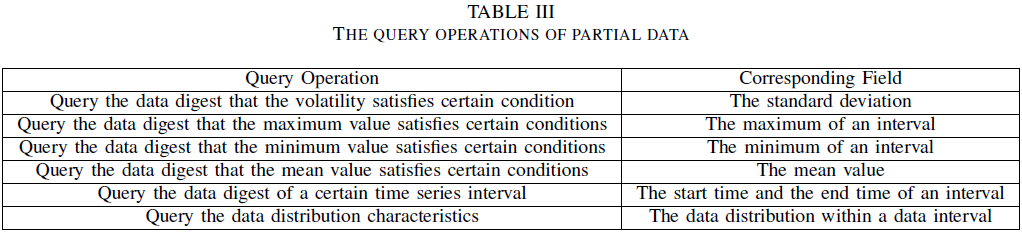
2-C. Data query

처리 후의 간격 데이터는 관계형 DB에 저장 ex) - 표 2
데이터의 특성 값에 따라 조회 가능
간격에는 시작 시간과 종료 시간이 있으므로 저장 형식은 시간 순서대로 데이터를 필터링하는 기준으로 제공
동시에 사용자는 특정 통계 값에 따라 데이터 쿼리 가능

3. The visualization of time series data

3-A Interval-based hierarchical visualization

데이터 전처리 후 데이터는 M 크기의 여러 데이터 간격으로 분리되어 관계형 데이터베이스에 저장되고 이에 기반하여 시각화된다.
대용량의 시계열 데이터는 압축되어도 여전히 많은 데이터 간격이 있다.
- 예) M = 100 (너무 작게)
  - 수백만 데이터가 수만 데이터 간격으로 전처리
  - 모든 데이터 간격이 표시되면 데이터 포인트가 너무 조밀
- 예) M = 10000 (너무 크게
  - 간격 수가 100개
  - 데이터의 로컬 특성 손실
병합의 세분성은 사용자의 요구에 따라 결정 가능하다.
데이터 전처리 후 초기 간격 데이터를 메타 간격 데이터로 정의
각 간격의 정의 : $R = <t_s, t_e, v_s, v_e, v_{max}, v_{min}, v_{avg}, v_{var}, E>$
데이터 시각화 단계
- 간격 크기를 kM (1 ≤ k)으로 설정
- 초기 간격 데이터에서 크기로 kM의 데이터 간격을 생성
병합된 메타 간격 중 i 번째 메타 간격은 $R_i = <t_{is}, t_{ie}, v_{is}, v_{ie}, v_{imax}, v_{imin}, v_{iavg}, v_{ivar}, Ei>로 표시
R의 각 값을 계산하는 방법(kM 값으로 구간의 특성 값 계산)
- $t_s = t_{1s}$ (식 3)
- $t_e = t_{ke}$ (식 4)
- $\alpha_s = v_{1s}$ (식 5)
- $\alpha_e = v_{ke}$ (식 6)
- $\alpha_{max} = max( v_{1max}, v_{2max}, ..., v_{kmax} ) $ (식 7)
- $\alpha_{min} = min( v_{1min}, v_{2min}, ... , v_{kmin} ) $ (식 8)
- $ \alpha_{avg} = 1/k \sum^k _{j=1} v_{javg} $ (식 9)
- $\alpha^2 _{var} = \sum^k _{j=1} v^2 _{javg} / k$ $+ \sum^k _{j=1}v^2 _{javr} /k$ $-(\sum^k _{j=1} v_{javg} )^2 /k^2 $ (식 10)
$v^2 _{ivar} = \sum^m _{j=1} x^2 _{ij} /M-v^2 _{iavg} $ (식 11)
- 분산의 기본 공식 단순화
- $x_{ij}$ : 병합할 k구간 중 i번째 구간의 j번째 데이터
- $x^2 _{ij}$ : 식 12의 오른쪽 첫 번째 항으로 대체 ( 실제 계산 과정 유추 불가)
$v^2 _{var} = \sum^k _{i=1} \sum^M _{j=1} x^2 _{ij} /kM - \alpha^2 _{avg} $ (식 12)
식 13은 식 11의 변환으로 구함
$\sum^k _{i=1} \sum^M _{j=1} x^2 _{ij}/kM = 1/k \sum^k _{i=1} v^2 _{ivar} -1/k \sum^k _{i=1} v^2 _{iavg} $ (식 13)

병합할 k 구간 중 i 번째 구간의 데이터 분포 벡터 $E_i$를 설정
- $e_{ij} (1 ≤ j ≤ P)$ : j 번째 값 구간의 데이터 수
- $(g_{(ij−1)}, g_{ij}]$ : j 번째 값 구간의 범위
병합하여 k 구간의 전체 데이터 분포
k 간격의 데이터 분포 벡터.
병합된 데이터 간격 $E = {e_j '| 1 ≤ j ≤ 10}$ 인 경우 새 값 간격의 범위는 $(g^\prime _{j−1}, g^\prime _ j)$이고 $g^\prime _0 = α_{min} − 1, g^\prime _10 = α_{max}$. C (x, y)는 구간 (x, y]의 데이터 수를 나타낸다.
함수 f ((y1, y2), (x1, x2)) 정의
- 간격 [y1, y2]에서 [x1, x2]까지의 데이터를 평균적으로 분배하고 간격 [x1, x2]의 데이터 수를 계산

$ e^{\prime} _i \sum^k _{i=1} \sum^{10} _{J=1} f((g_{ij-1} , g_i j), (g^{\prime} _{j-1} , g^{\prime} _j )) $ (식 15)

식 15를 통해 모든 간격이 합병된 데이터 셋$E^{\prime}$ 을 얻음

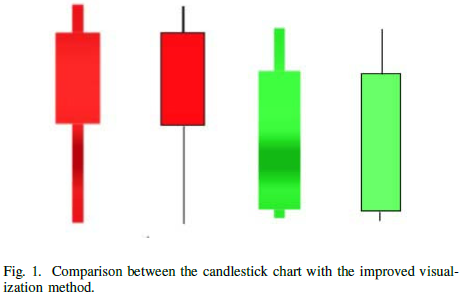
3-B The improved visualization method of candlestick chart

촛대 차트
- 일정 기간 동안의 제품 가격 변동 추세 반영
- 데이터 분석 및 추세 예측 시 자주 사용
- 데이터 변경 과정 및 추세를 명확하게 표현 가능
- 특정 기간의 데이터 분포 설명 표현에 어려움
- 여러 시간 단위로 형성된 K-라인으로 구성
- 가로 축 - 시간 / 세로 축 - 가격 or 포인트로 구성
- ex ) 주식 시장 시스템
  - 각 사이클의 시가, 최고 가격, 최저 가격 및 종가를 분석하여 캔들 차트 생성

촛대 차트와 열역학 다이어그램을 결합하여 촛대 차트의 최대 값과 최소값 사이의 색 농도를 통해 고정 데이터 간격 내 변화의 데이터 분포 표현

4. Experiments and comparative analysis

4-A Experimental analysis of time series data visualization

자동차 주행 방향 가속 테스트
- 상태 모니터링, 고장 조기 경보 및 진단을 실현하기 위해 차량 전송 장치에 많은 센서를 설치하고 센서에 의해 수집된 데이터는 전송 장치의 차량 테스트 중 호스트 컴퓨터로 지속적으로 전송
- 수집 된 데이터에는 기어 및 방향, 엔진 속도, 엔진 반환 수온, 팬 속도 등 40 개 매개 변수가 포함
- 초당 10회 샘플링 속도로 장치는 1시간 동안 지속적으로 실행될 때 24000개의 데이터 레코드를 수집
- 이러한 데이터를 실험 기반으로 사용하고 시계열 데이터 시각화 시스템을 사용하여 이러한 데이터를 시각화
본 논문에서는 다른 차원에 따라 간격을 나누어 비교하여 성능을 테스트하고 원본 데이터에 해당하는 그림 2와 그림 6과 같이 변동 범위가 다른 두 종류의 데이터를 선택하여 실험한다.

200의 간격으로 시각화된 데이터 // 데이터가 상대적으로 매끄럽고 급격한 변동이 없으며 일반적인 추세가 가끔씩 감소하는 것을 확인 가능

400의 간격으로 시각화된 데이터 // 데이터가 상대적으로 매끄럽고 급격한 변동이 없으며 일반적인 추세가 가끔씩 감소하는 것을 확인 가능

800의 간격으로 시각화된 데이터 // 데이터가 상대적으로 매끄럽고 급격한 변동이 없으며 일반적인 추세가 가끔씩 감소하는 것을 확인 가능

간격 값 - 필요한 연속 값 수

그림 3, 4, 5에 따르면 캔들 스틱 차트는 데이터의 변동을 매우 잘 보여주고 원본 차트의 로컬 데이터의 극적인 변동과 대조를 이루며 원본 데이터의 변동 복원이 가능하고 데이터의 전반적 특성 또한 매우 잘 보존된다. 또한 데이터 압축률(간격)이 증가하면 데이터의 국지적 급격한 변동이 감소한다.

Fig. 7, 8, 9는 각각 200,400, 800 구간 값의 데이터 시각화 결과에 해당
3가지 시각화 결과는 모두 상승 추세를 보이고 있으며 로컬 구간의 감소는 좋은 보존으로 복원 가능
데이터 압축률이 증가함에 따라 데이터의 로컬 특성이 손실되지만 전체적인 변동에는 영향을 미치지 않음

4-B Comparative analysis

시계열 데이터의 압축을 위해 많은 연구자들은 특성 데이터를 압축하는 방법 제시

이 논문에서는 시계열 (선택적 특징점에 기반한 PLR, 나중에 PLR_EFP라고 함)을 기반으로 기상 데이터 압축 알고리즘 선택
- PLR_EFP
- 특징점의 선택을 기반으로 하는 분할 알고리즘
- 먼저 데이터 시리즈의 극단 점과 추세 전환점을 선택한 다음 필터링 규칙에 따라 선택한 특징점 필터링
- 선택한 지점의 처음 K개 데이터 지점과 선택한 지점의 마지막 K개 데이터 지점인 경우의 포인트가 특징 포인트가 아닌 경우 선택한 포인트가 예약 그렇지 않으면 필터링
  - K : 알고리즘에서 미리 설정된 매개 변수
4.1 및 PLR_EFP의 실험 통계를 사용하고 다른 매개 변수 K값을 설정하여 여러 비교 실험을 수행
- 그림 10과 그림 11은 서로 다른 파라미터 K값에서 기어 및 핸들(방향)의 데이터 압축 결과 표현
- 그림 12와 그림 13은 서로 다른 매개 변수 K값에서 엔진 수온 데이터 압축 결과 표현
변동이 심한 데이터의 경우 파라미터 K 값이 증가하면 심각한 데이터 손실이 발생
느리게 변하는 데이터의 경우 데이터 감소 정도 ↑

큰 변동이 있는 데이터의 경우 K 값이 증가시 간격 특성 손실
- 그림 10, 11
  - K 값이 9로 증가하면 PLR_EFP 알고리즘 이후 큰 변동이있는 압축 데이터가 손실됨
- 그림 3
  - 데이터 저장의 입도가 상대적으로 크지 만 데이터의 휘발성을 잃지 않음

동일한 데이터 세트의 PLR EFP 알고리즘과 PLR DIF 알고리즘으로 압축 한 후 데이터 막대 번호의 대비 표시

PLR DIF 데이터 압축률이 PLR EFP보다 훨씬 높다
실험 결과에 따르면 촛대 차트를 기반으로 한 시계열 데이터 시각화 방법은 데이터의 전반적인 특성을 잘 보존
데이터 압축률이 증가함에 따라 데이터의 일부 로컬 특성이 손실되지만 전체적인 변동성은 여전히 잘 나타난다.

시계열 데이터 시각화 방법은 주로 조각 별 선형 표현 기호 표현 주파수 영역 표현 및 특잇값 표현을 포함한다.
시계열 데이터는 2차원 평면의 곡선이며 PLR (piece-wise linear representation)은 끝에서 끝까지 선 세그먼트를 사용하여 곡선을 대략적으로 나타내므로 직관적이고 효율적으로 매우 일반적인 방법이다.
이러한 방법의 초기 연구 결과는 PAA (Piecewise Aggregation averaging method)로 시퀀스를 여러 세그먼트로 나누고 각 세그먼트의 평균값을 사용하여 데이터를 나타낸다.
최근 연구 결과는 추세 전환점, 중요점, 연속적인 조각 별 다항식 모델 등과 같은 방법을 기반으로 한다
- 조각 별 선형 표현에서 가장 중요한 부분은 분할 지점을 결정하는 것입니다.

PAA
- 시퀀스를 균등하게 나누고 방법을 개선하는 것
trend 전환점 방법을 기반으로 시계열 데이터의 극단점과 변곡점을 트렌드 전환점으로 찾고, 트렌드 전환점을 대체 세분화 점으로 정의한 다음 점 사이의 거리로 선택하여 영역, 주어진 임계 값에 따라 최종 분할 지점을 얻습니다.
중요한 점 방법의 경우, 중요한 점 탐지 기술을 사용하여 일련의 중요한 점을 알아내지만, 횡단 이진트리를 사용하여 적절한 중요한 점을 세분화 점으로 얻습니다.
시계열 데이터에 대한 이러한 종류의 시각화 방법은 훨씬 더 직관적이지만 편차가 상대적으로 크고 조각 별 다항식 모델 표현 [13] [14] [15]은 편차가 더 작으며 시계열 데이터를 세분화하고 하위 시퀀스에 적합하도록 간단한 다항식 함수를 사용하므로 더 잘 적합할 수 있다.

원래의 시계열 데이터를 더 잘 맞추기 위해 조각상 선형 표현은 하향 알고리즘, 상향 알고리즘, 슬라이딩 윈도우 등을 사용한다.
- 탑다운 알고리즘
  - 글로벌에서 로컬로 먼저 시작점과 끝점을 알아낸 뒤 중간점을 찾아낸다
- 상향식 알고리즘
  - 하향식 알고리즘과 반대로 시계열 데이터는 짧은 시퀀스로 나눈 다음, 압축률이 낮은 이 작은 적합 편차점으로부터 적절한 점을 얻는다.
  - 오차는 매우 작지만 여러 점을 하나의 점으로 결합하는 것과 동등한 오른쪽 점 저점의 압축률이다.
- 슬라이딩 윈도우 방법
  - 윈도우의 크기를 결정하는 일정한 임계값을 부여한 다음, 윈도우의 움직임에 따라 일정 범위 동안 반복되어 필요하지 않은 시간 지점을 제거하여 더 나은 시간 분할을 얻는 것이다.
이러한 방법들은 시계열 데이터의 추세를 생생하게 묘사하기 위해 조각별 구간을 사용하며, 이를 바탕으로 데이터를 분석 및 예측하고 특정 시간 간격의 최고값, 최솟값, 평균값, 표준편차와 같은 데이터 특성을 얻기 위해, 본 논문에서는 촛대 차트를 기초로 한 표현 방법을 제안한다.
촛대 도표 촛대 차트는 주식시장과 선물시장에서 매우 흔하며 개시 가격, 최고가, 최저가, 종가 등으로 그려진다.
이를 바탕으로 평균값과 표준편차와 같은 데이터 특성이 추가되어 이 방법은 시계열 데이터의 실제 변화를 철저히 관찰하는 데 도움이 된다.

5. Summary

본 논문은 빅 데이터 시대의 방대한 시계열 데이터를 빠르게 처리할 수 있는 캔들 스틱 차트를 기반으로 대용량 시계열 데이터의 다이제스트를 빠르게 생성하고 시각화하는 방법을 제시
각 데이터 간격에서 추출된 통계 데이터는 간격의 특성을 반영 가능
계산된 데이터는 캔들 스틱 차트, 꺾은 선형 차트 등을 통해 사용자에게 피드백되므로 사용자가 데이터의 특성을 직접 파악 가능
이 시스템은 대용량 데이터에 대한 처리 능력이 뛰어나며 시각적 효과가 분명하여 다양한 단계에서 데이터의 변동성을 직접 반영 가능
데이터의 원본 정보가 완전히 보존

저작자표시 비영리 변경금지

하나씩 화이팅!!